A high-dimensional sphere spilling out of a high-dimensional cube despite exponentially many constraints
Make a square, split each side into two halves, producing four cells. Put a circle into each cell such that it fills it completely. There is a small gap right in the middle of the square. Put a circle there again such that it touches the other four circles. The central circle is obviously inside the square, right? Yes, but only if the dimension you are in is $D\le9$. Above that, the central cicle actually spills out from the cube, despite the $2^D$ spheres in their cells keeping it in. In this post I present this simple-to-compute yet utterly counter-intuitive result.
Stanislav Fort (Twitter, Scholar and GitHub)
Let’s do it step by step:
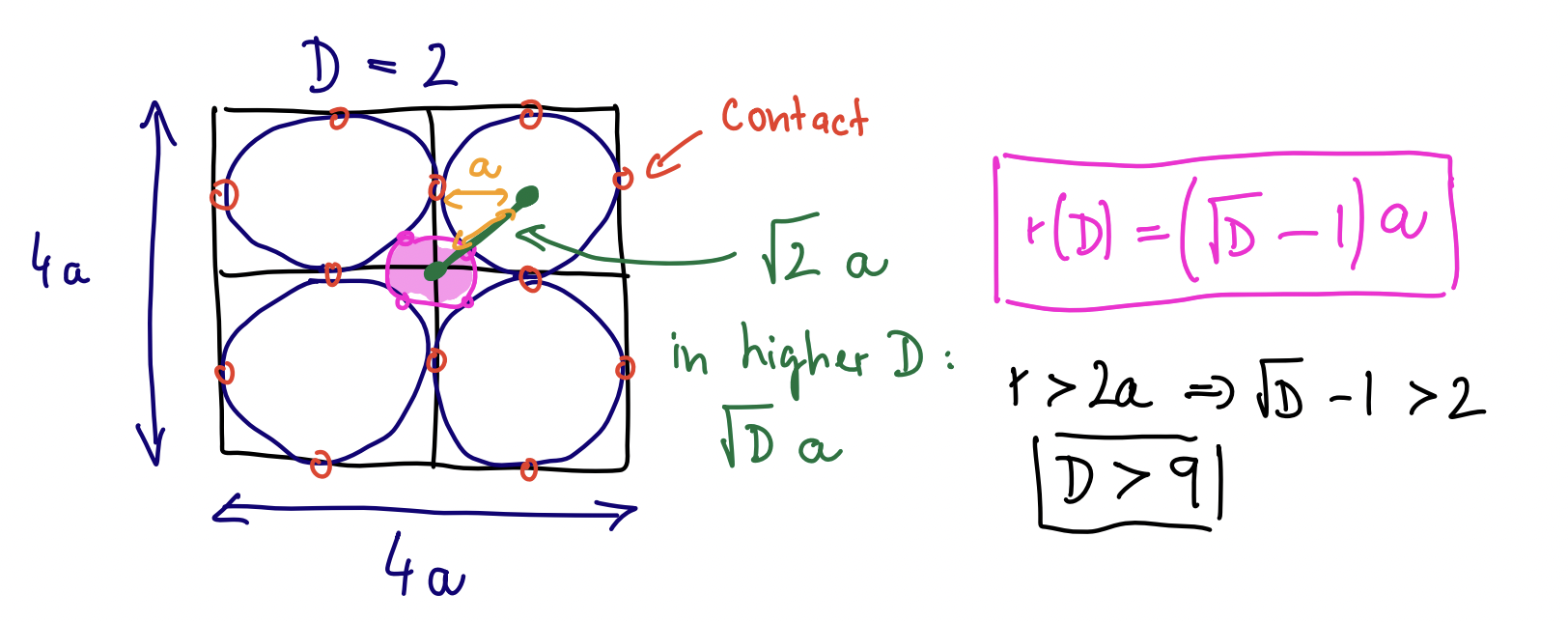
- Make a square of an edge length $4a$ (the 4 will make our life easier later).
- Divide each side into two halves. This will produce 4 equal cells in two dimesions, or $2^D$ cells in $D$-dimensions.
- Put a circle (two dimensions) / sphere ($D$-dimensions) to each cell to fill it up completely. Each sphere will touch the walls of the cell and will therefore have a radius $\rho=a$. There will be $2^D$ such spheres in $2^D$ cells.
- Put a circle as big as possible to the exact center of the square / cube such that it touches all $2^D$ spheres. This will uniquelly determine its radius. In two dimensions, this circle is obviously inside the square, right?
- The distance from the center of the square to the center of each cell is $\sqrt{2}$a in two dimensions, or $\sqrt{D}a$ in $D$-dimensions. The reason for this is that it is a $1/4$ of the full diagonal of the cube, which is generically $\sqrt{D} \times 4a$.
- The distance from the center of the cube to the center of each cell must be the sum of the radius of the inner sphere $r$ and the radius of the cell-filling sphere $\rho=a$, since these two touch by definition. Therefore $\sqrt{D}a = a + r(D)$.
- This implies that $\boxed{r(D) = \left ( \sqrt{D} - 1 \right ) a}$ .
So far, nothing seems to be intuitively wrong. For $D=2$, we get the radius of the central circle to be $r(D=2) = (\sqrt{2}-1) a$, which is smaller than $2a$, the half-size of the square. Therefore the central circle is indeed nicely contained within the square. All is good.
Notice, however, that $r(D)$ is monotonic and unbounded from above in $D$. This means that as the dimension grows, the central sphere will grow in radius, while the linear size of the cube stays the same. At some point, the sphere must stick out of the cube! And it isn’t even such a high dimension you need for that to be the case: $r(D) > 2a \implies D > 9$.
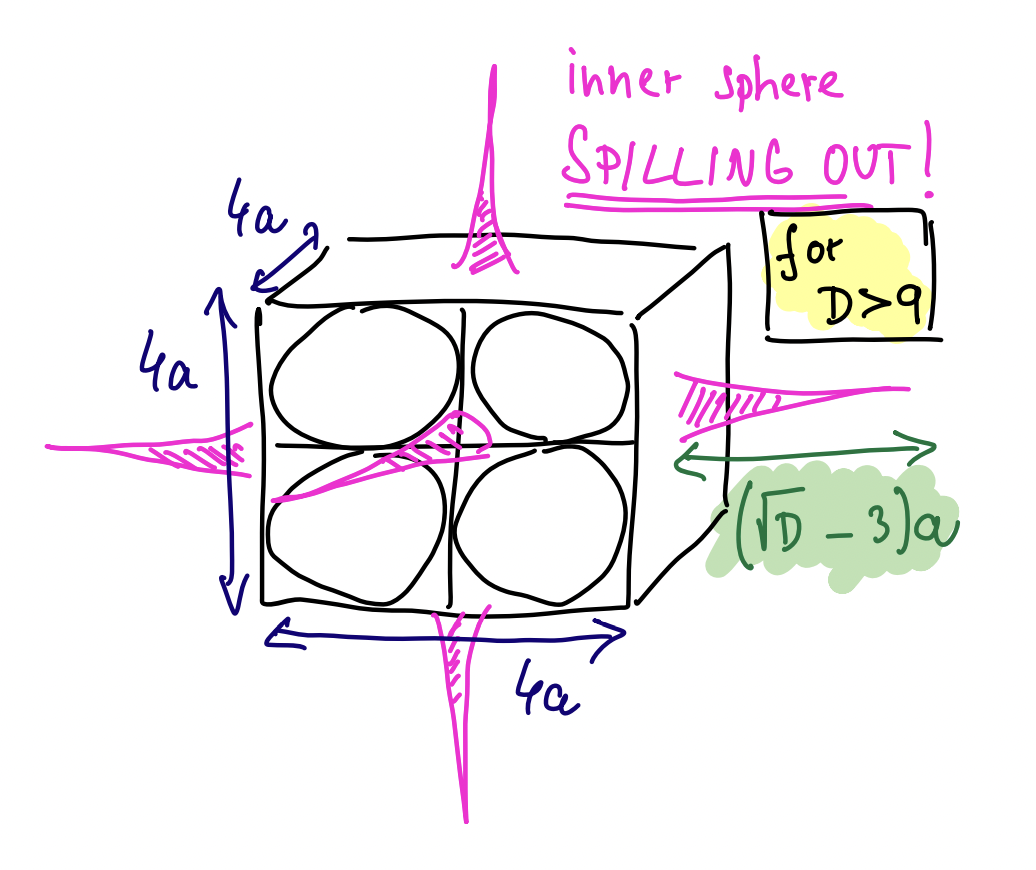
For dimension $D>9$, the simplified, three-dimensional-turned-two-dimensional mental picture is of a cube from which parts of the inner sphere are sticking out through the middles of the cube walls.
This is a pretty intuitively unnerving result for me! It also goes against an intuitely strong principle that an exponential number of constraints (here the $2^D$ spheres in their respective cells) should be sufficient to constrain things even in high dimensions. On a vague level, this reminds of the recent Basins with tentacles paper by Yuanzhao Zhang and Steven H. Strogatz.